 /
/ 
Time Limit: 2 sec / Memory Limit: 256 MB
配点 : 800 点
問題文
縦 R 行、横 C 列のマス目があります。 上から r 行目、左から c 列目にあるマスを (r,c) と呼びます。
高橋君は N 箇所のマスに非負整数を書き込みました。 具体的には、各 1≤i≤N について、マス (r_i,c_i) に非負整数 a_i を書き込みました。 その後、高橋君は居眠りを始めました。
マス目を見つけた青木君は、残りすべてのマスに整数を書き込み、高橋君を驚かせようとしています。 高橋君を驚かせるためには、マス目が次の条件を満たさなければなりません。
- 条件 1 : 各マスには非負整数が書き込まれている。
- 条件 2 : 縦 2 行、横 2 列の正方形をどこから取り出しても、(左上の整数) + (右下の整数) = (右上の整数) + (左下の整数) が常に成り立つ。
残りすべてのマスに書き込む整数を工夫することで、マス目が条件を満たすようにできるか判定してください。
制約
- 2≤R,C≤10^5
- 1≤N≤10^5
- 1≤r_i≤R
- 1≤c_i≤C
- (r_i,c_i) はすべて相異なる。
- a_i は整数である。
- 0≤a_i≤10^9
入力
入力は以下の形式で標準入力から与えられる。
R C N r_1 c_1 a_1 r_2 c_2 a_2 : r_N c_N a_N
出力
残りすべてのマスに書き込む整数を工夫することで、マス目が条件を満たすようにできるならば、Yes を出力せよ。
できないならば、No を出力せよ。
入力例 1
2 2 3 1 1 0 1 2 10 2 1 20
出力例 1
Yes
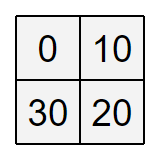
図のように整数を書き込めばよいです。
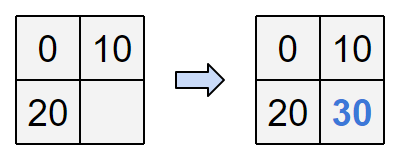
入力例 2
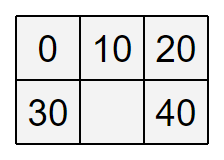
2 3 5 1 1 0 1 2 10 1 3 20 2 1 30 2 3 40
出力例 2
No
マス目には次の 2 個の正方形があります。
- マス (1,1),(1,2),(2,1),(2,2) からなる正方形
- マス (1,2),(1,3),(2,2),(2,3) からなる正方形
左側の正方形において条件 2 が成り立つためには、空きマスの整数は 40 でなければなりません。 すると、右側の正方形において条件 2 が成り立たなくなります。
入力例 3
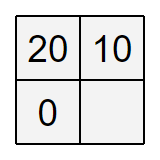
2 2 3 1 1 20 1 2 10 2 1 0
出力例 3
No
条件 2 が成り立つためには、空きマスの整数は -10 でなければなりません。 すると、条件 1 が成り立たなくなります。
入力例 4
3 3 4 1 1 0 1 3 10 3 1 10 3 3 20
出力例 4
Yes
例えば、図のように整数を書き込めばよいです。
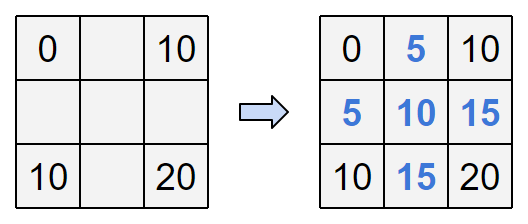
入力例 5
2 2 4 1 1 0 1 2 10 2 1 30 2 2 20
出力例 5
No
既にすべてのマスに整数が書き込まれており、条件 2 が成り立っていません。
Score : 800 points
Problem Statement
There is a grid with R rows and C columns. We call the cell in the r-th row and c-th column (r,c).
Mr. Takahashi wrote non-negative integers into N of the cells, that is, he wrote a non-negative integer a_i into (r_i,c_i) for each i (1≤i≤N). After that he fell asleep.
Mr. Aoki found the grid and tries to surprise Mr. Takahashi by writing integers into all remaining cells. The grid must meet the following conditions to really surprise Mr. Takahashi.
- Condition 1: Each cell contains a non-negative integer.
- Condition 2: For any 2×2 square formed by cells on the grid, the sum of the top left and bottom right integers must always equal to the sum of the top right and bottom left integers.
Determine whether it is possible to meet those conditions by properly writing integers into all remaining cells.
Constraints
- 2≤R,C≤10^5
- 1≤N≤10^5
- 1≤r_i≤R
- 1≤c_i≤C
- (r_i,c_i) ≠ (r_j,c_j) (i≠j)
- a_i is an integer.
- 0≤a_i≤10^9
Input
The input is given from Standard Input in the following format:
R C N r_1 c_1 a_1 r_2 c_2 a_2 : r_N c_N a_N
Output
Print Yes if it is possible to meet the conditions by properly writing integers into all remaining cells.
Otherwise, print No.
Sample Input 1
2 2 3 1 1 0 1 2 10 2 1 20
Sample Output 1
Yes
You can write integers as follows.

Sample Input 2
2 3 5 1 1 0 1 2 10 1 3 20 2 1 30 2 3 40
Sample Output 2
No
There are two 2×2 squares on the grid, formed by the following cells:
- Cells (1,1), (1,2), (2,1) and (2,2)
- Cells (1,2), (1,3), (2,2) and (2,3)
You have to write 40 into the empty cell to meet the condition on the left square, but then it does not satisfy the condition on the right square.

Sample Input 3
2 2 3 1 1 20 1 2 10 2 1 0
Sample Output 3
No
You have to write -10 into the empty cell to meet condition 2, but then it does not satisfy condition 1.

Sample Input 4
3 3 4 1 1 0 1 3 10 3 1 10 3 3 20
Sample Output 4
Yes
You can write integers as follows.

Sample Input 5
2 2 4 1 1 0 1 2 10 2 1 30 2 2 20
Sample Output 5
No
All cells already contain a integer and condition 2 is not satisfied.
